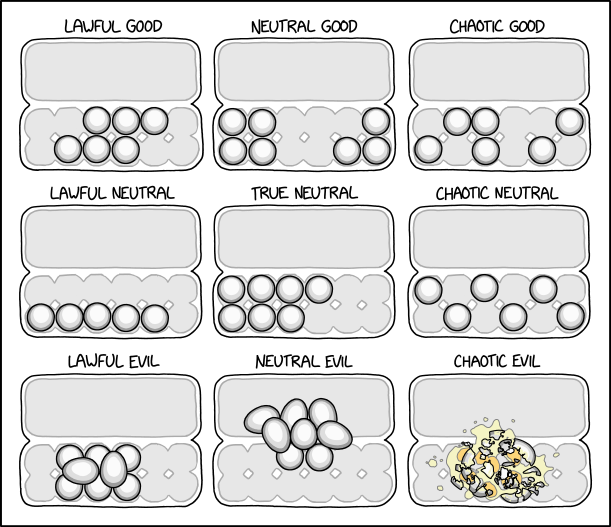

I would be Lawful Neutral, if not for the fact that I want to leave the suspicious looking eggs until last which makes me Chaotic Good in reality.
Neutral Evil is for people who like keeping the weight nicely centered in the carton, but also hate everyone else who wants that.
6 public comments
I switch between Lawful Good/Chaotic Neutral.
I think Chaotic Neutral and Chaotic Good should be swapped though. First of all, Chaotic Good is more random than Chaotic Neutral, which doesn't add up. Also, the choice for "chaotic" neutral still follows a pattern, and has some practical use: the weight is evenly divided over the carton.
I think Chaotic Neutral and Chaotic Good should be swapped though. First of all, Chaotic Good is more random than Chaotic Neutral, which doesn't add up. Also, the choice for "chaotic" neutral still follows a pattern, and has some practical use: the weight is evenly divided over the carton.

Alan Watts gave an interesting talk on what you might do if you had an eternity of time to fill:
http://project.unicorn.holtof.com/watts/from_time_to_eternity.htm
> You would want a surprise. After all, what are we trying to do with our technology - we are trying to control the world. And if you will imagine the ultimate fulfillment of technology, when we really are in control of everything, and we have great panels of push buttons whereon the slightest touch will fulfill every wish, you will eventually arrange to have a special red button on it marked "surprise."
http://project.unicorn.holtof.com/watts/from_time_to_eternity.htm
> You would want a surprise. After all, what are we trying to do with our technology - we are trying to control the world. And if you will imagine the ultimate fulfillment of technology, when we really are in control of everything, and we have great panels of push buttons whereon the slightest touch will fulfill every wish, you will eventually arrange to have a special red button on it marked "surprise."
2 public comments
A favorite rumination along these subjects for me remains 17776. https://www.sbnation.com/a/17776-football
Louisville, Kentucky
Beautiful, but since this is Existential Comics:
> you can feel what I can never feel
... didn't he just argue that he exhausts all possible feelings before eternity is over?
What if all possible feelings create an infinite set? Is that set smaller than eternity?
(I wonder if mathematicians who study infinities have any interesting ideas about living for an eternity)
> you can feel what I can never feel
... didn't he just argue that he exhausts all possible feelings before eternity is over?
What if all possible feelings create an infinite set? Is that set smaller than eternity?
(I wonder if mathematicians who study infinities have any interesting ideas about living for an eternity)
Next Page of Stories








